常见的十种排序算法及时间复杂度测试

算法是一个长期积累的过程，需要不断地练习与锤炼，很难一蹴而就。与框架不同，算法不会过时，从长远来看，更具实用价值。

在公司的面试中，算法题目是常见的考察内容，这要求我们持续不断地练习，通过刷题来提升解题思维和算法能力。许多注重算法能力的公司，如谷歌、字节跳动等，都将算法作为面试的重要考核项。

话不多说，先来一个开胃菜。

二分（折半）查找

• 在这之前，需要先解释几个位运算：>>、>>>、|

  • >>：算术右移，它会将二进制数（包括符号位）整体右移，通常用于正整数。>> 也可以用来替代 Math.floor()，实现向下取整的效果。
  • >>>：逻辑右移，它只对数值位进行右移，符号位不会改变，适用于负数。>>> 也可以用来代替 Math.floor()，实现向下取整的效果。
  • |：按位或操作，它将两个数的每一位（二进制位）进行比较，0 | 1 = 1，0 | 0 = 0。常用 | 0 来代替 Math.trunc()，将浮点数向零取整。
  • 从纯性能角度来看，逻辑移位因为不涉及符号位的处理，性能略优于算术移位。

• 二分查找算法假设数组是有序的，每次通过选择数组中间的元素与目标值进行比较：

  • 如果两者相等，返回该元素的下标；
  • 如果目标值小于中间元素，则在数组的左半部分继续查找；
  • 如果目标值大于中间元素，则在数组的右半部分继续查找。

• 对应：leetcode-704题

function binarySearch(arr: number[], target: number): number {
  let left = 0, right = arr.length - 1;

  while (left <= right) {
    // const mid = (left + right) >>> 1;
    // 如果 left 和 right 是大整数，使用上式可能会导致溢出。这是 C++ 和 Java 中的编码习惯
    const mid = left + ((right - left) >> 1);
    if (target === arr[mid]) {
      return mid;
    } else if (target > arr[mid]) {
      left = mid + 1;
    } else {
      right = mid - 1;
    }
  }
  return -1;
}

冒泡排序（Bubble Sort）

• 冒泡排序是一种简单的排序算法：

  • 基本思路是通过比较相邻元素并交换它们的位置，将较大的元素逐渐“冒泡”到序列的末尾，直到整个序列有序。
  • 每进行一趟排序，最大的元素会被移动到数组的最后，因此可以忽略已排序的部分，减少不必要的比较。
  • 不断重复此过程，直到数组完全排序。

• 冒泡排序图解

  
  ts

  function bubbleSort(arr: number[]): number[] {
    let n = arr.length;
    while (n > 0) {
      // 记录最后一次交换的位置
      let lastSwapIndex = 0;
      for (let i = 1; i < n; i++) {
        if (arr[i - 1] > arr[i]) {
          // 交换两个元素
          [arr[i - 1], arr[i]] = [arr[i], arr[i - 1]];
          lastSwapIndex = i;
        }
      }
      // 最后一次交换的位置之后的元素已经有序，不需要再次排序
      n = lastSwapIndex;
    }
    return arr;
  }

选择排序（Selection Sort）

• 选择排序（Selection Sort）是一种简单的排序算法：

  • 在未排序的数列中找到最小（或最大）元素，并将其交换到数列的起始位置；
  • 然后，在剩余的未排序部分中继续找到最小（或最大）元素，并将其放到已排序部分的末尾；
  • 重复以上过程，直到所有元素都排序完毕。

• 选择排序图解

  
  ts

  /**
   * 选择排序
   * 1. 选择排序是一种原地排序算法，不稳定排序算法
   * 2. 选择排序的时间复杂度是O(n^2)
   * 3. 选择排序的思路是：在每一轮中，找到最小值，然后依次放到已排序队列的后面
   */
  function selectionSort(arr: number[]): number[] {
    const n = arr.length;
    // 前面的 n-1 个元素都找到了最小值，最后一个元素不需要再找
    for (let i = 0; i < n - 1; i++) {
      // 记录最小值的索引
      let minIndex = i;
      for (let j = i + 1; j < n; j++) {
        if (arr[j] < arr[minIndex]) {
          minIndex = j;
        }
      }
      // 如果最小值的索引不是i，说明找到了更小的值，交换位置
      if (minIndex !== i) {
        [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
      }
    }
    return arr;
  }

插入排序（Insertion Sort）

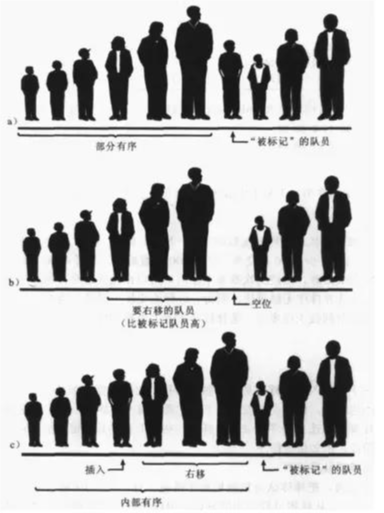
• 插入排序的流程如下：

  • 假设数组的第一个元素已排好序，单元素数组默认有序。

  • 从第二个元素开始，与前面的有序部分进行比较。

  • 如果当前元素小于前面的元素，则插入到正确的位置。

  • 重复此过程，直到整个数组有序。

• 插入排序图解

  
  ts

  /**
   * 插入排序
   * 1.插入排序是一种原地排序算法，稳定排序算法
   * 2.插入排序的时间复杂度是O(n^2)
   * 3.插入排序的思路是：
   *    将数组分为已排序区间和未排序区间，初始时已排序区间只有第一个元素
   *    依次取未排序区间的元素，与已排序区间元素比较，若小于前者则交换，直到找到合适位置
   */
  function insertionSort(arr: number[]): number[] {
    const n = arr.length;
    // 外层循环的作用：从第二个元素开始，第一个元素默认有序
    for (let i = 1; i < n; i++) {
      // 依次和前面的元素比较，如果小于前面的元素，则交换位置
      for (let j = i; j > 0; j--) {
        if (arr[j - 1] > arr[j]) {
          [arr[j - 1], arr[j]] = [arr[j], arr[j - 1]];
        } else {
          // 如果不小于前面的元素，则说明已找到合适的位置，后续不需要再进行比较
          break;
        }
      }
    }
    return arr;
  }

归并排序（Merge Sort）

• 归并排序的思路（分治思想）

• 步骤一：分解（Divide）

  • 若待排序数组长度为 1，则认为该数组已排序，直接返回。
  • 将待排序数组分为两个长度相等的子数组，对每个子数组递归进行归并排序。
  • 合并两个排好序的子数组，返回一个有序数组。

• 步骤二：合并（Merge）

  • 使用两个指针分别指向两个子数组的起始位置，比较它们的元素，将较小的元素插入新数组。
  • 若一个子数组已遍历完，将另一个子数组的剩余元素直接加入新数组。
  • 返回这个已排序的新数组。

• 归并排序图解

  
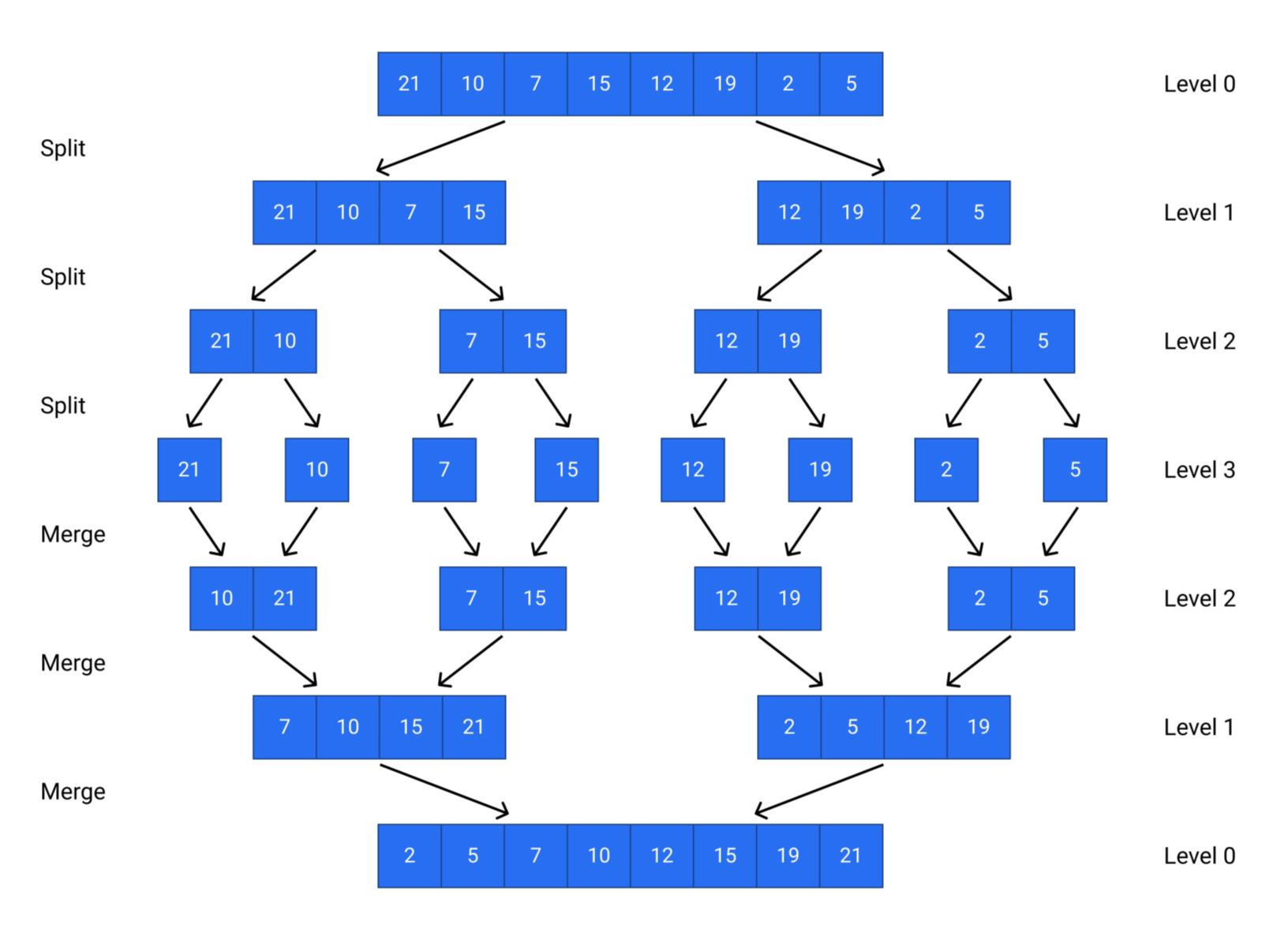  ts

  /**
   * 归并排序(分治思想)：
   * 时间复杂度：O(nlogn)
   * 空间复杂度：O(n)，可以优化到 O(logn)，即原地归并排序（in-place merge sort）
   * 归并排序的思路是：
   *    递归地将数组二分，直到每个子数组的长度为1，然后按照顺序合并两个有序子数组，直到合并为一个完整的有序数组。
   */
  function mergeSort(arr: number[]): number[] {
    const n = arr.length;
    mergeSortInternal(arr, 0, n - 1);
    return arr;
  }
  
  // 归并排序内部实现函数，对数组 arr 的子区间 [left, right] 进行排序
  function mergeSortInternal(arr: number[], left: number, right: number): void {
    // 递归终止条件：子区间只有一个元素
    if (left >= right) return;
  
    const mid = left + ((right - left) >>> 1);
    // 递归对左右两个子区间进行排序
    mergeSortInternal(arr, left, mid);
    mergeSortInternal(arr, mid + 1, right);
    // 将排好序的左右两个子区间进行合并
    merge(arr, left, mid, right);
  }
  
  // 将已排好序的左右两个子区间合并成一个有序的区间
  function merge(arr: number[], left: number, mid: number, right: number): void {
    const temp: number[] = [];
    // k 用于记录 temp 数组的索引
    let i = left, j = mid + 1, k = 0;
  
    // 比较左右两个子区间的元素，将较小的元素插入到 temp 中
    while (i <= mid && j <= right) {
      if (arr[i] <= arr[j]) {
        temp[k++] = arr[i++];
      } else {
        temp[k++] = arr[j++];
      }
    }
  
    // 如果左子区间还有元素，将它们全部复制到 temp 中
    while (i <= mid) {
      temp[k++] = arr[i++];
    }
  
    // 如果右子区间还有元素，将它们全部复制到 temp 中
    while (j <= right) {
      temp[k++] = arr[j++];
    }
  
    // 将 temp 中的元素复制回原数组
    for (let p = 0; p < k; p++) {
      arr[left + p] = temp[p];
    }
  }

快速排序（Quick Sort）

• 快速排序的流程可以分为以下几步：

  • 选择一个基准元素，通常是第一个或最后一个元素。

  • 定义两个指针 i 和 j，分别指向数组的两端。

  • 从左侧开始，移动指针 i，找到第一个大于或等于基准元素的值。

  • 从右侧开始，移动指针 j，找到第一个小于或等于基准元素的值。

  • 如果 i 小于或等于 j，交换 i 和 j 指向的元素。

  • 重复步骤 3-5，直到 i 超过 j，此时交换基准元素与 j 指向的元素，将基准元素放到中间位置。

  • 将数组划分为左右两个部分，左侧包含小于或等于基准的元素，右侧包含大于基准的元素。

  • 对左右两部分递归执行快速排序，直到每部分仅剩一个元素。

  • 最终，整个数组将变为有序。

• 快速排序图解

  
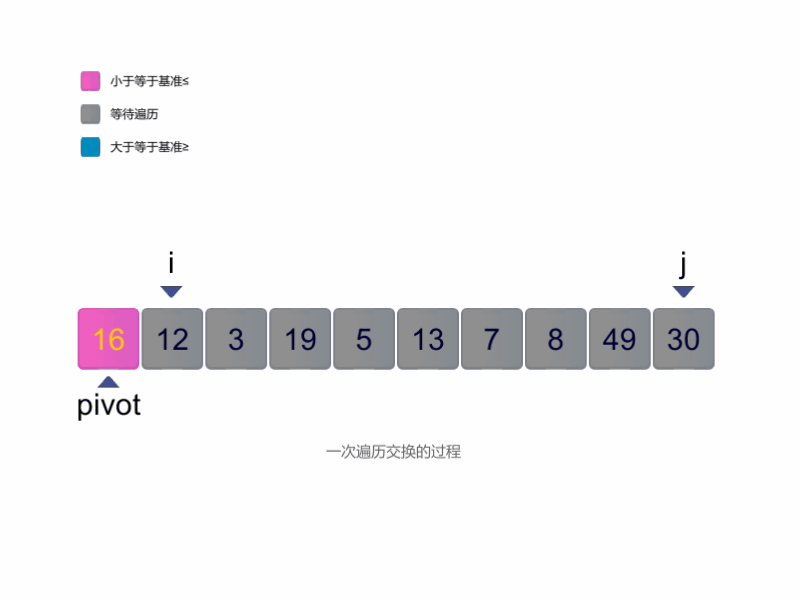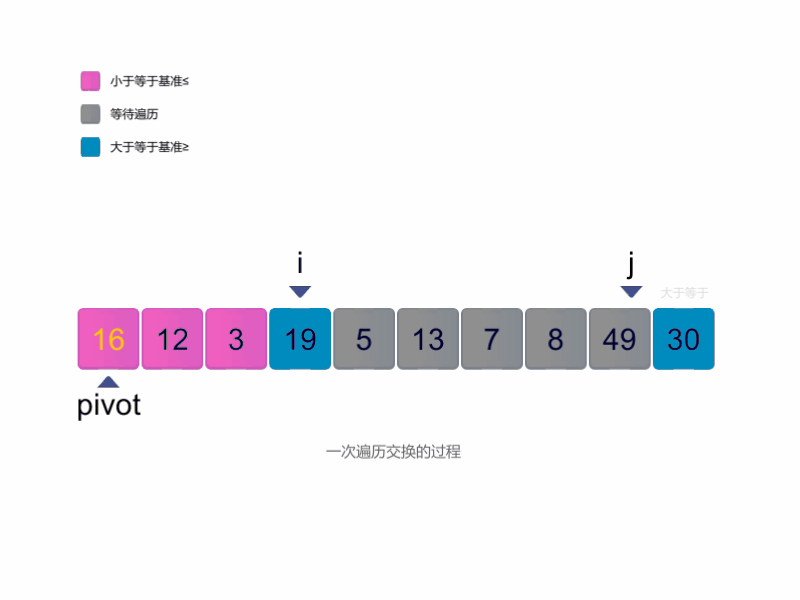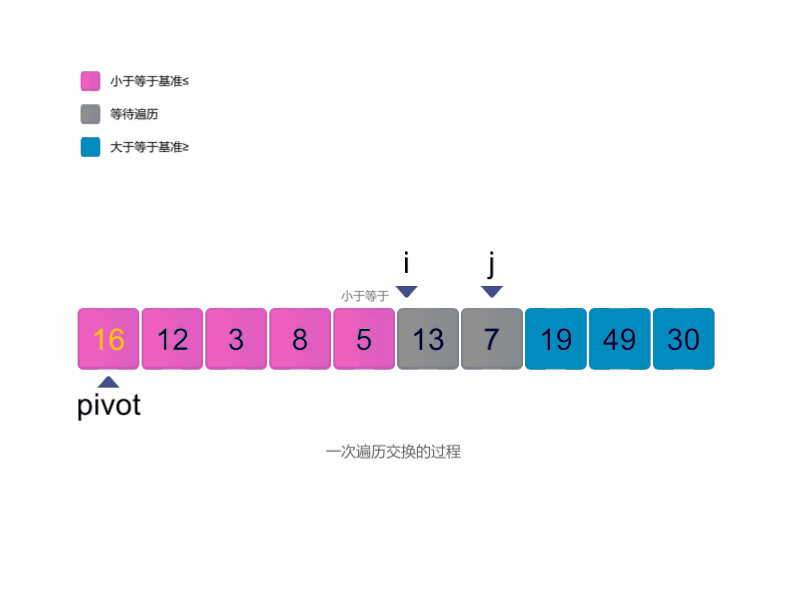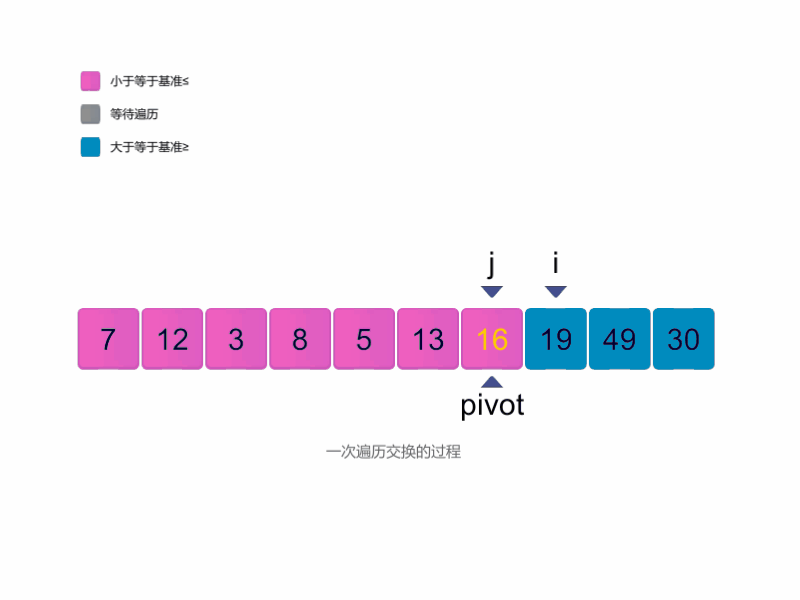  ts

  /**
   * 快速排序(分治思想)
   * 时间复杂度：O(nlogn)，最坏情况下时间复杂度为 O(n^2)
   * 空间复杂度：O(logn)
   */
  function quickSort(arr: number[]): number[] {
    partition(0, arr.length - 1);
  
    function partition(left: number, right: number): void {
      // 左指针大于等于右指针，说明已经划分完成
      if (left >= right) return;
  
      let i = left + 1, j = right;
      const pivot = arr[left];
  
      while (i <= j) {
        // i往右开始找，找到比pivot更大或者相等的值
        while (arr[i] < pivot) i++;
        // j往左开始找，找到比pivot更小或者相等的值
        while (arr[j] > pivot) j--;
        // 到这里有两种情况
        // 要么是i和j都找到了合适的值（需要交换两个元素）
        // 要么就是i和j所指向的元素相等，并且等于pivot的值（需要继续向前移动，实际上不会发生交换）
        if (i <= j) {
          [arr[i], arr[j]] = [arr[j], arr[i]];
          i++;
          j--;
        }
      }
      // 如果到达这里，说明i已经大于j，此时需要交换pivot和j所指的元素
      [arr[left], arr[j]] = [arr[j], arr[left]];
  
      // 继续划分左右区域
      // 因为上一次 j 和 pivot 交换了位置，所以当前 j 的位置是 pivot，因此需要 j - 1
      partition(left, j - 1);
      partition(i, right);
    }
    return arr;
  }

• 快速排序的优化：

  ts

  /**
   * 优化的快速排序算法：
   *   1.原地排序：避免了使用额外的数组空间，通过交换元素的位置来排序
   *   2.三数取中法：选择枢轴(基准)时，使用三数取中法选择枢轴，避免极端情况下的退化
   *   3.插入排序优化：当子数组的长度小于阈值时，使用插入排序以提高性能
   * @param array 待排序的数组
   * @param left 数组的左边界索引，默认为0
   * @param right 数组的右边界索引，默认为数组长度减一
   * @returns 已排序的数组
   */
  function optimizedQuickSort(array: number[], left = 0, right = array.length - 1): number[] {
    // 当子数组的长度小于此阈值时，使用插入排序
    const INSERTION_SORT_THRESHOLD = 10;
  
    // 如果子数组的长度小于阈值，使用插入排序以提高性能
    if (right - left < INSERTION_SORT_THRESHOLD) {
      insertionSort(array, left, right);
    } else {
      // 确保左索引小于右索引，防止递归溢出
      if (left < right) {
        // 使用三数取中法选择枢轴，并将其放置到合适的位置
        const pivotIndex = medianOfThree(array, left, right);
        // 对数组进行分区，返回枢轴的最终位置
        const partitionIndex = partition(array, left, right, pivotIndex);
        // 对左子数组递归进行快速排序
        optimizedQuickSort(array, left, partitionIndex - 1);
        // 对右子数组递归进行快速排序
        optimizedQuickSort(array, partitionIndex + 1, right);
      }
    }
    // 返回已排序的数组
    return array;
  }
  
  /**
   * 插入排序算法
   * @param array 待排序的数组
   * @param left 排序的起始索引
   * @param right 排序的结束索引
   */
  function insertionSort(array: number[], left: number, right: number): void {
    // 从子数组的第二个元素开始遍历
    for (let i = left + 1; i <= right; i++) {
      const key = array[i]; // 当前要插入的元素
      let j = i - 1;
      // 向左遍历已排序部分，找到合适的位置插入key
      while (j >= left && array[j] > key) {
        array[j + 1] = array[j]; // 将比key大的元素向右移动一位
        j--;
      }
      array[j + 1] = key; // 将key插入到正确的位置
    }
  }
  
  /**
   * 三数取中法选择枢轴
   * @param array 待排序的数组
   * @param left 左边界索引
   * @param right 右边界索引
   * @returns 枢轴的索引
   */
  function medianOfThree(array: number[], left: number, right: number): number {
    const center = (left + right) >>> 1; // 计算中间索引
  
    // 将左、中、右三个元素进行排序
    if (array[left] > array[center]) {
      [array[left], array[center]] = [array[center], array[left]]; // 交换左和中
    }
    if (array[left] > array[right]) {
      [array[left], array[right]] = [array[right], array[left]]; // 交换左和右
    }
    if (array[center] > array[right]) {
      [array[center], array[right]] = [array[right], array[center]]; // 交换中和右
    }
  
    // 将枢轴（中间值）移动到右边界前一位的位置
    [array[center], array[right - 1]] = [array[right - 1], array[center]];
    return right - 1; // 返回枢轴的索引
  }
  
  /**
   * 分区函数
   * @param array 待分区的数组
   * @param left 左边界索引
   * @param right 右边界索引
   * @param pivotIndex 枢轴的索引
   * @returns 分区后枢轴的最终位置
   */
  function partition(array: number[], left: number, right: number, pivotIndex: number): number {
    const pivot = array[pivotIndex]; // 获取枢轴的值
    let i = left; // 初始化左指针
    let j = right - 1; // 初始化右指针（因为枢轴在 right - 1 位置）
  
    while (true) {
      // 从左向右找到第一个大于等于枢轴的元素
      while (array[++i] < pivot) {}
      // 从右向左找到第一个小于等于枢轴的元素
      while (array[--j] > pivot) {}
      // 当左指针与右指针交错时，退出循环
      if (i >= j) break;
      // 交换左指针和右指针所指的元素
      [array[i], array[j]] = [array[j], array[i]];
    }
  
    // 将枢轴移动到正确的位置
    [array[i], array[right - 1]] = [array[right - 1], array[i]];
    return i; // 返回枢轴的最终位置
  }

堆排序（Heap Sort）

• 在理解堆排序之前，需要先了解二叉堆（包括最大堆和最小堆），它们也称为大顶堆和小顶堆。React 中的调度器 Scheduler 就使用最小堆排序算法来实现任务调度。在这里，我们以最大堆为例讲解堆排序，最小堆的原理类似。

• 解释两个概念：下沉（下滤）和上浮（上滤）

  • 下沉：用于从上到下调整节点位置，以维持堆的性质。常见于删除堆顶元素后重新调整堆。
  • 上浮：用于从下到上调整节点位置，以维持堆的性质。常见于插入新元素后调整堆。

• 堆排序的两个主要步骤：构建最大堆和排序

• 构建最大堆

  • 从待排序数组的最后一个非叶子节点 floor(length / 2) - 1 开始，依次对每个节点进行调整。
  • 对于节点索引 i，左子节点的索引为 2i + 1，右子节点的索引为 2i + 2，父节点的索引为 (i - 1) / 2。
  • 对每个节点 i，将其与左右子节点的值进行比较，找到其中最大的值，并将其与节点 i 交换。
  • 重复以上步骤，直到节点 i 满足最大堆的性质。
  • 按此方式对每个非叶子节点操作，直到根节点，最终构建出一个最大堆。

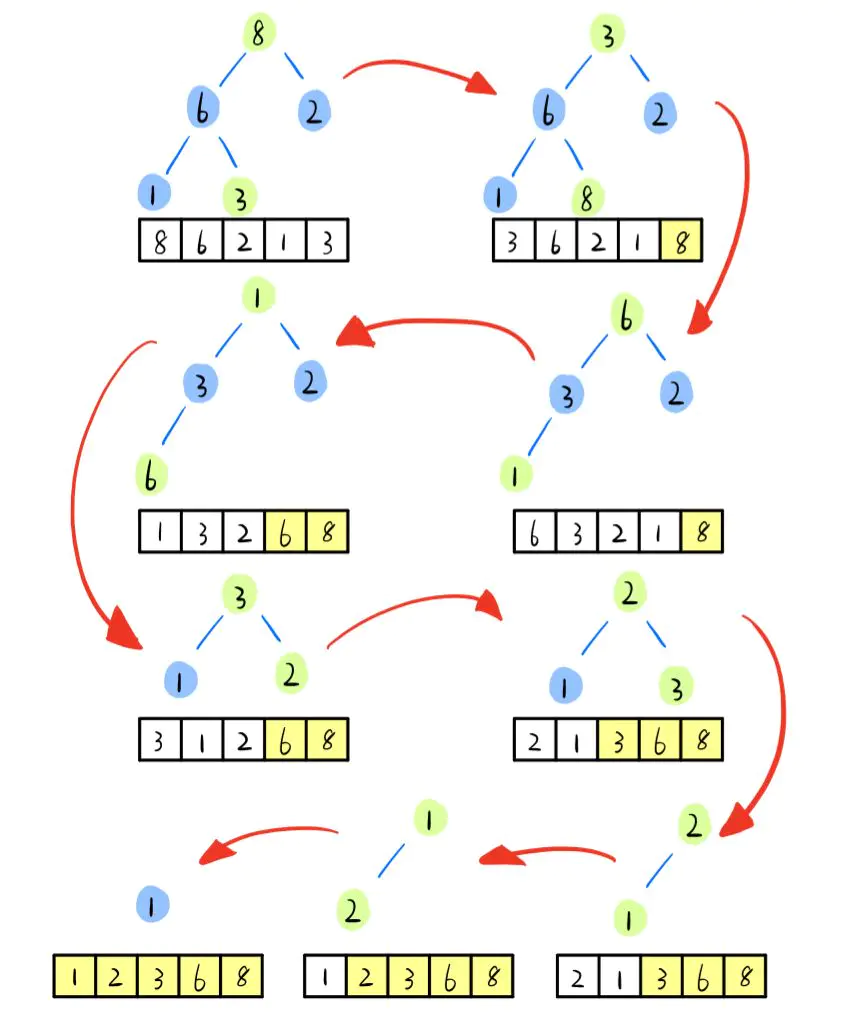
• 排序

  • 将堆的根节点（即最大值）与堆的最后一个元素交换，使最大值被放到正确的位置。
  • 缩小堆的范围，并将剩余的元素重新构建成一个最大堆。
  • 重复步骤 1 和步骤 2，直到堆的大小缩小到 1，即完成排序。

• 最大堆排序图解

  
  ts

  /**
   * 堆排序
   *    1.堆排序是一种选择排序，它的最坏、最好、平均时间复杂度均为O(nlogn)。
   *    2.堆排序是不稳定的排序算法。
   *    3.堆排序的空间复杂度为O(1)，是一种原地排序算法。
   */
  function heapSort(arr: number[]): number[] {
    const n = arr.length;
  
    // 1. 原地建最大堆
    for (let i = (n >>> 1) - 1; i >= 0; i--) {
      heapifyDown(arr, n, i); // 从最后一个非叶节点开始下沉
    }
  
    // 2. 交换堆顶元素与末尾元素，缩小堆的范围，然后重新调整最大堆
    for (let i = n - 1; i > 0; i--) {
      [arr[0], arr[i]] = [arr[i], arr[0]]; // 将堆顶（最大值）交换到末尾
      heapifyDown(arr, i, 0); // 调整堆，使剩余部分继续保持最大堆
    }
  
    return arr;
  }
  
  /**
   * 最大堆的下沉操作，构建或维护最大堆
   * @param arr 需要进行下沉操作的数组
   * @param length 当前堆的范围（数组的长度）
   * @param index 当前节点的索引
   */
  function heapifyDown(arr: number[], length: number, index: number): void {
    let i = index;
  
    // 当存在左子节点时继续循环（没有左子节点说明没有子节点）
    while (2 * i + 1 < length) {
      const leftChildIndex = 2 * i + 1;
      const rightChildIndex = 2 * i + 2;
      let largerChildIndex = leftChildIndex; // 默认最大值为左子节点
  
      // 判断是否存在右子节点，且右子节点的值大于左子节点
      if (rightChildIndex < length && arr[rightChildIndex] > arr[leftChildIndex]) {
        largerChildIndex = rightChildIndex;
      }
  
      // 如果当前节点大于等于左右子节点中的较大值，停止下沉
      if (arr[i] >= arr[largerChildIndex]) {
        break;
      }
  
      // 交换当前节点与较大的子节点
      [arr[i], arr[largerChildIndex]] = [arr[largerChildIndex], arr[i]];
  
      // 更新当前节点的索引为较大子节点的索引
      i = largerChildIndex;
    }
  }

希尔排序（Shell Sort）

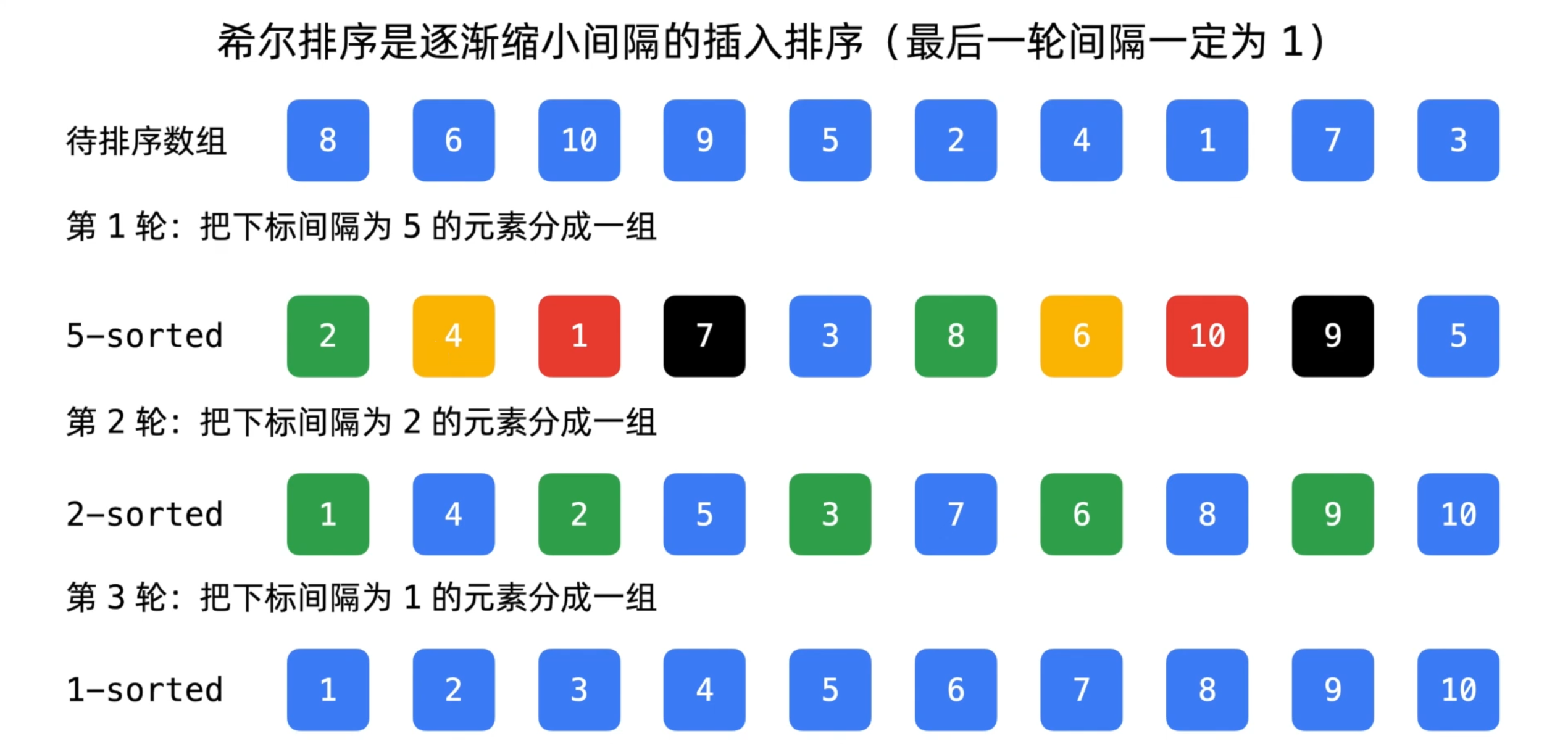
• 希尔排序利用分组插入排序的思想，通过不断缩小间隔，让数据逐步趋于有序。其步骤如下：

  • 定义一个增量序列 d1, d2, ..., dk，其中最后一个增量为 1（即 dk = 1）。
  • 以 dk 为间隔，将待排序数组划分为若干子序列，对每个子序列分别进行插入排序。
  • 逐步减小增量 dk，对每次划分的子序列进行插入排序，直至增量为 1。

• 希尔排序图解

  
  ts

  /**
   * 希尔排序
   *    1.希尔排序是插入排序的一种更高效的改进版本，它的实质就是分组插入排序
   *    2.希尔排序是非稳定排序算法
   *    3.时间复杂度：O(nlogn) ~ O(n²)，空间复杂度：O(1)，是一种原地排序算法
   * 希尔排序的基本思想是：
   *    - 先将整个待排序的记录序列(按照增量序列)分割成为若干子序列分别进行直接插入排序
   *    - 待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序
   *    - 增量(步长/间隔)序列：tk = n / 2^k，其中n为数组长度，k为增量序列的索引，最后一个增量值必须为1
   */
  function shellSort<T>(arr: T[]): T[] {
    const n = arr.length;
    let gap = n >>> 1; // 初始化增量
  
    while (gap > 0) {
      for (let i = gap; i < n; i++) {
        const temp = arr[i];
        let j = i;
  
        // 插入排序，将 temp 插入到当前分组的正确位置
        while (j >= gap && arr[j - gap] > temp) {
          arr[j] = arr[j - gap];
          j -= gap;
        }
  
        arr[j] = temp;
      }
      gap >>>= 1; // 缩小增量
    }
    return arr;
  }

计数排序（Counting Sort）

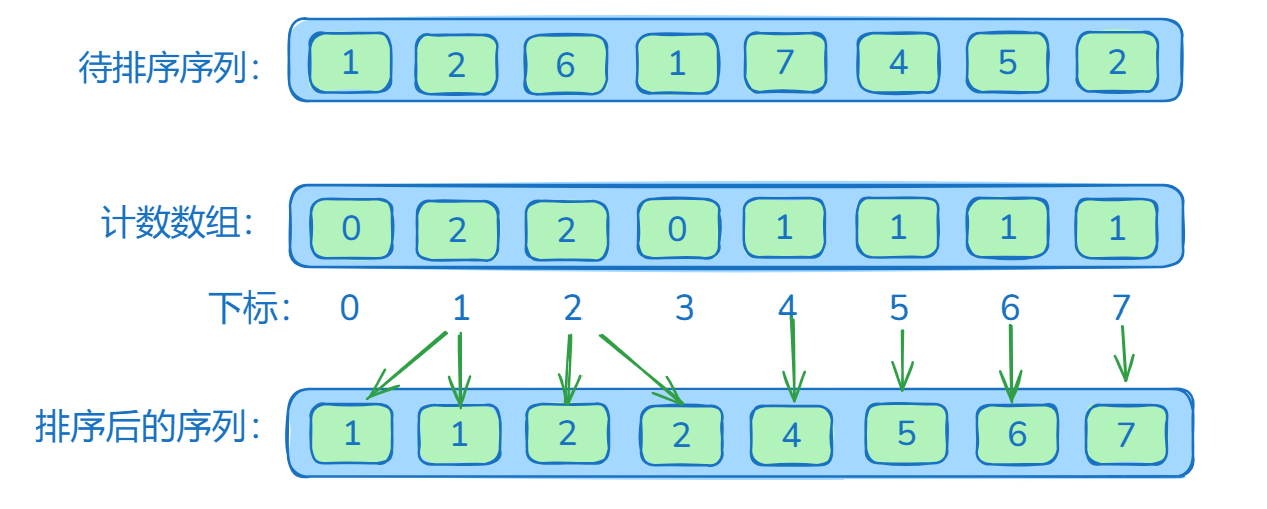
• 计数排序是一种非比较的排序算法，适用于数据范围较小的正整数数组。当元素值的范围较小时，计数排序的时间复杂度为 O(n+k)，其中 k 是数据的数值范围，效率非常高。其基本步骤如下：

• 统计元素频次：

  • 遍历原始数组，找到数组中的最大值和最小值，确定计数数组的大小。
  • 创建一个计数数组 count，其长度为 max - min + 1，初始化所有元素为 0。
  • 遍历原始数组，统计每个元素出现的次数，将其存入计数数组对应的索引位置。

• 累加计数数组：

  • 对计数数组进行累加操作，使每个位置的值表示原始数组中小于或等于该索引的元素个数。

• 回填排序结果：

  • 创建一个结果数组 output，用于存放排序结果。
  • 反向遍历原始数组，根据计数数组中的值确定每个元素在结果数组中的位置，同时将计数数组对应的值减 1。

• 输出结果：

  • 将排序后的数组复制回原始数组或直接返回结果数组。

• 计数排序图解

  
  ts

  /**
   * 计数排序
   *    1.计数排序是一种用空间换时间的排序算法
   *    2.计数排序是一种高效的排序算法，但由于其空间复杂度较高，因此不适合在数据范围较大的场景中使用
   *    3.时间复杂度：O(n + k)，空间复杂度：O(n + k)，是一种稳定的排序算法
   */
  function countingSort(arr: number[]): number[] {
    const n = arr.length;
  
    // 计算数列最大值和最小值
    let max = arr[0];
    let min = arr[0];
    for (let i = 1; i < n; i++) {
      if (arr[i] > max) {
        max = arr[i];
      }
      if (arr[i] < min) {
        min = arr[i];
      }
    }
  
    // 统计数列中每个值出现的次数
    const count = new Array(max - min + 1).fill(0);
    for (const num of arr) {
      count[num - min]++; // 偏移 min，使索引从 0 开始
    }
  
    // 累加数组
    for (let i = 1; i < count.length; i++) {
      count[i] += count[i - 1];
    }
  
    // 从后向前遍历原始数组，按照统计数组中的位置放置元素
    const res = new Array(n);
    for (let i = n - 1; i >= 0; i--) {
      res[--count[arr[i] - min]] = arr[i];
    }
  
    return res;
  }

桶排序 Bucket Sort

• 桶排序是一种分配排序算法，通过将数据分布到多个桶中，再对每个桶进行单独排序，最终合并结果来完成排序。其基本步骤如下：

  • 确定最大值和最小值：找到数组中的最大值和最小值，用于划分桶的范围。
  • 确定桶的数量：根据 bucketSize 和数组的范围计算需要的桶数。
  • 分配元素到桶：通过计算每个元素的桶索引，将其放入对应的桶中。
  • 桶内排序：对每个桶内的元素进行排序（使用插入排序或快速排序等）。
  • 合并结果：将所有桶内的已排序元素按顺序合并到结果数组中。

• 桶排序图解

  
  ts

  /**
   * 桶排序
   *    1.桶排序是一种分配排序算法，利用桶的划分将数据分布到多个区间中再排序
   *    2.桶排序适用于数据分布均匀且范围已知的场景，但对数据范围过大或分布不均的场景不太适用
   *    3.时间复杂度：O(n + k)，空间复杂度：O(n + k)，其中k是桶的数量，是一种稳定的排序算法（取决于桶内排序算法）
   */
  function bucketSort(arr: number[], bucketSize = 5) {
    if (arr.length === 0) {
      return arr;
    }
  
    // 找到数组中的最大值和最小值
    let i: number;
    let minValue = arr[0];
    let maxValue = arr[0];
    for (i = 1; i < arr.length; i++) {
      if (arr[i] < minValue) {
        minValue = arr[i];
      } else if (arr[i] > maxValue) {
        maxValue = arr[i];
      }
    }
  
    // 计算桶的数量
    let bucketCount = (((maxValue - minValue) / bucketSize) | 0) + 1;
    let buckets = new Array(bucketCount);
    for (i = 0; i < buckets.length; i++) {
      buckets[i] = [];
    }
  
    // 将数组中的元素分配到各个桶中
    for (i = 0; i < arr.length; i++) {
      buckets[((arr[i] - minValue) / bucketSize) | 0].push(arr[i]);
    }
  
    // 对每个桶中的元素进行排序
    arr.length = 0;
    for (i = 0; i < buckets.length; i++) {
      if (buckets[i].length > 0) {
        insertionSort(buckets[i]);
        for (let j = 0; j < buckets[i].length; j++) {
          arr.push(buckets[i][j]);
        }
      }
    }
  
    return arr;
  }
  
  // 插入排序
  function insertionSort(arr: number[]) {
    const n = arr.length;
    for (let i = 1; i < n; i++) {
      for (let j = i; j > 0; j--) {
        if (arr[j - 1] > arr[j]) {
          [arr[j - 1], arr[j]] = [arr[j], arr[j - 1]];
        } else {
          break;
        }
      }
    }
    return arr;
  }

基数排序（Radix Sort）

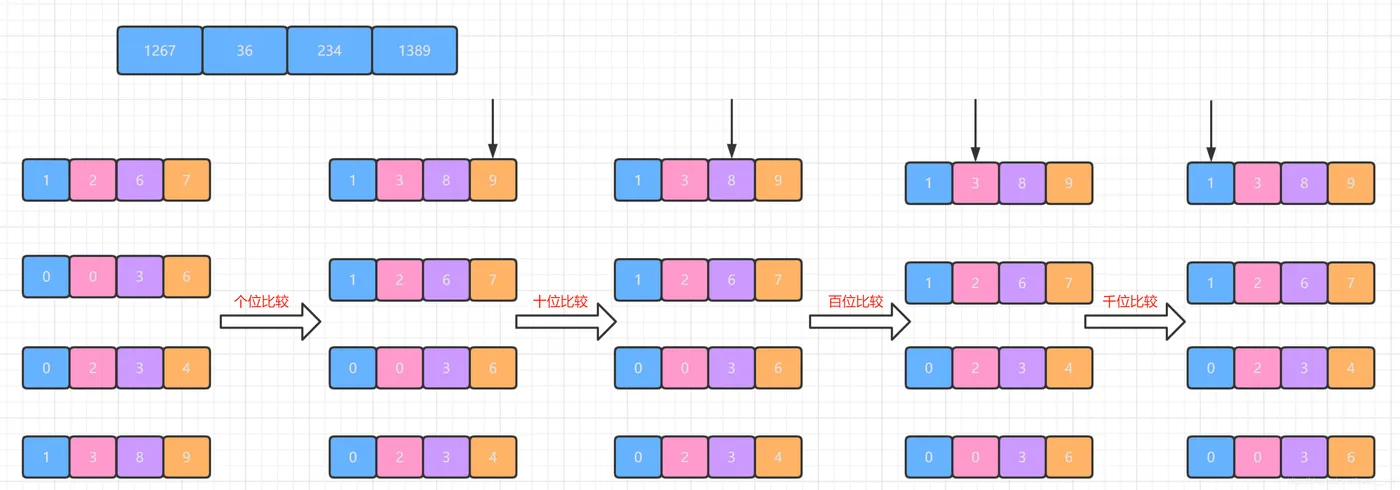
• 基数排序是一种非比较排序算法，主要适用于整数或者字符串的排序。它按照数位（个位、十位、百位等）依次进行排序，利用稳定性排序算法将数据按位排序，最终实现整体有序。

• 基数排序的思路

  • 找出数组中最大数，确定其包含的位数 d，这决定了需要排序的轮数。
  • 从最低位（个位）开始，一直到最高位，每一位使用稳定的排序算法（如计数排序或桶排序）对数据进行排序。
  • 每轮排序后，数据根据当前位数有序，下一轮基于更高一位进行排序，直至最高位。

• 基数排序图解

  
  ts

  /**
   * 基数排序
   * 基数排序是一种非比较型排序算法，按照数字的每一位进行排序（从低位到高位）。
   * 每一轮排序使用稳定的排序算法（计数排序或桶排序）对当前位进行排序。
   * 时间复杂度：O(d * (n + k))，其中d是位数，n是元素个数，k是基数（通常为10）。
   * 空间复杂度：O(n + k)，其中n是数组长度，k是基数。
   */
  function radixSort(arr: number[]): number[] {
    if (arr.length === 0) return arr;
  
    // 找到最大值以确定最大位数
    const maxNum = Math.max(...arr);
    const maxDigit = (Math.log10(maxNum) | 0) + 1;
  
    // 从个位到最高位排序
    let place = 1; // 初始为个位
    for (let i = 0; i < maxDigit; i++) {
      // 按当前位进行桶排序
      arr = bucketSort(arr, place);
      place *= 10; // 处理下一位
    }
  
    return arr;
  }
  
  /**
   * 使用桶排序对数组按指定位数排序
   * @param arr 要排序的数组
   * @param place 当前位数（个位、十位等）
   * @returns 排序后的数组
   */
  function bucketSort(arr: number[], place: number): number[] {
    const buckets: number[][] = Array.from({ length: 10 }, () => []); // 创建10个桶
  
    // 将数字分配到桶中
    for (let num of arr) {
      const digit = ((num / place) % 10) | 0; // 提取当前位的数字
      buckets[digit].push(num); // 将数字放入对应的桶
    }
  
    // 合并所有桶中的数据
    return ([] as number[]).concat(...buckets);
  }

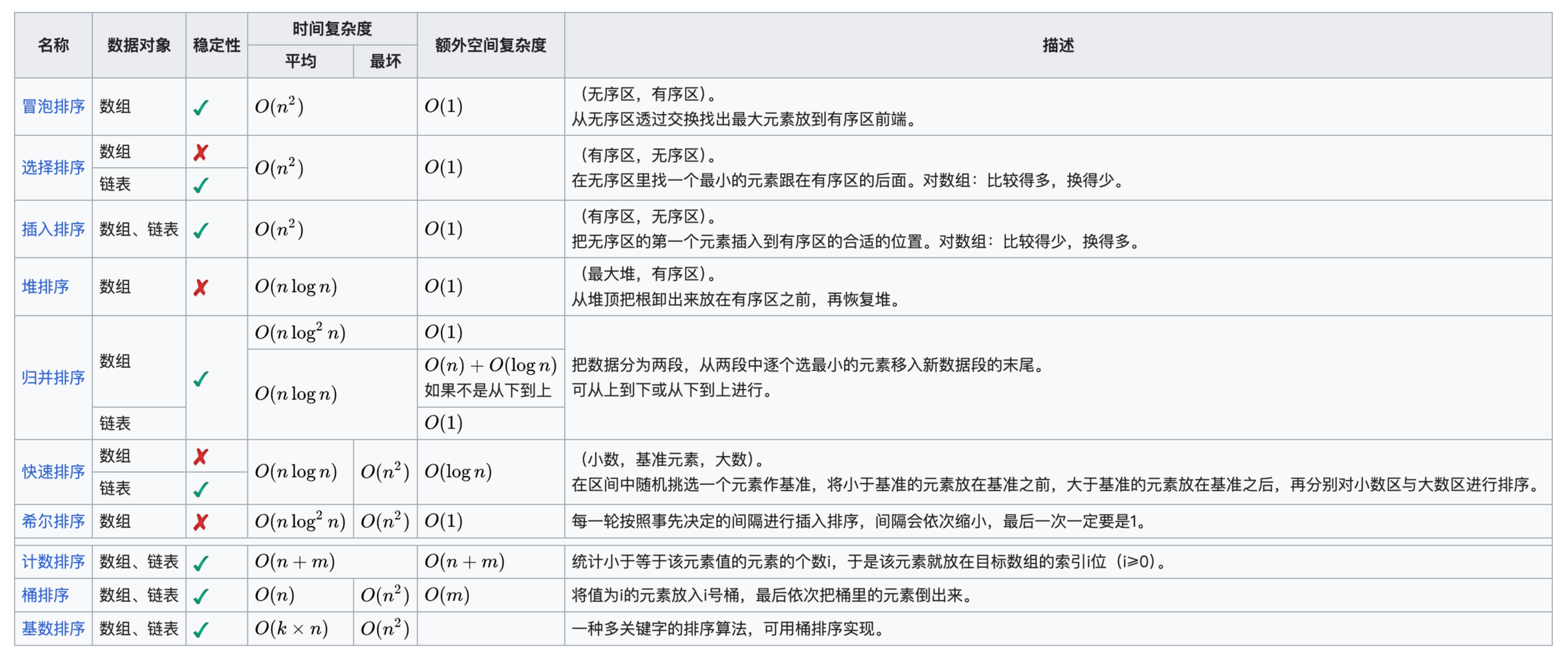
排序算法的复杂度和稳定性总结

十种排序算法时间测试

在搭载 M2 Pro 的 macOS 系统上进行测试，随机数范围为 0 到 999999，数据量为 10 万。我们测试了十种常见的排序算法，并加入了优化版快速排序。以下是测试结果（结果仅供参考，不同测试可能略有差异）。

写在最后：下一期我们来聊聊JavaScript、Java、Python底层都在使用的排序算法：TimSort